Análise do dataset
Flor de Íris
O conjunto de dados flor de Íris ou conjunto de dados Íris de Fisher é um conjunto de dados multivariados introduzido pelo estatístico e biólogo britânico Ronald Fisher em seu artigo de 1936, "O uso de múltiplas medições em problemas taxonômicos", como um exemplo de análise discriminante linear. Fonte: Wikipedia.
Conjunto Flor de Íris
Às vezes, é chamado de conjunto de dados da íris de Anderson porque Edgar Anderson coletou os dados para quantificar a variação morfológica das flores da íris de três espécies relacionadas. Fonte: Wikipedia.O simbolismo desse dataset para a área de dados
O conjunto de dados da íris é amplamente usado como um conjunto de dados para iniciantes para fins de aprendizado de máquina. O conjunto de dados está incluído no R (linguagem de programação) base e no Python pacote de aprendizado de máquina Scikit-learn, para que os usuários possam acessá-lo sem precisar encontrar uma fonte para ele. Fonte: Wikipedia.O dataset é formado por 150 registros em 5 colunas.
iris.shape
(150, 5)
O conjunto de dados contém 150 registros e consiste em 50 amostras de cada uma das três espécies de Iris ( Iris setosa, Iris virginica e Iris versicolor), um terço cara pada uma.
print(iris['Species'].value_counts())
Iris-setosa 50 Iris-versicolor 50 Iris-virginica 50 Name: Species, dtype: int64
plt.pie(iris['Species'].value_counts().values, labels=iris['Species'].unique(),autopct='%1.1f%%')
plt.show()
Quatro variáveis foram medidas em cada amostra: o comprimento e a largura das sépalas e pétalas, em centímetros.
iris.columns
Index(['SepalLengthCm', 'SepalWidthCm', 'PetalLengthCm', 'PetalWidthCm',
'Species'],
dtype='object')
Estatísticas gerais por espécie catalogada
Conhecer as estatísticas gerais é uma boa maneira de se obter uma visão panorâmica de um conjunto de dados. Nesse dataset, pressupôe-se que as correlações entre as variáveis em estudo se dão por espécie, assim, inicialmente tratamos cada uma como um conjunto separado.Quantidade, média, desvio padrão, mínimo, quartil 25%, mediana, quartil 75% e valor máximo de cada característica para a variante Iris setosa:
iris.loc[iris['Species'] == 'Iris-setosa'].describe()
| SepalLengthCm | SepalWidthCm | PetalLengthCm | PetalWidthCm | |
|---|---|---|---|---|
| count | 50.00000 | 50.000000 | 50.000000 | 50.00000 |
| mean | 5.00600 | 3.418000 | 1.464000 | 0.24400 |
| std | 0.35249 | 0.381024 | 0.173511 | 0.10721 |
| min | 4.30000 | 2.300000 | 1.000000 | 0.10000 |
| 25% | 4.80000 | 3.125000 | 1.400000 | 0.20000 |
| 50% | 5.00000 | 3.400000 | 1.500000 | 0.20000 |
| 75% | 5.20000 | 3.675000 | 1.575000 | 0.30000 |
| max | 5.80000 | 4.400000 | 1.900000 | 0.60000 |
Quantidade, média, desvio padrão, mínimo, quartil 25%, mediana, quartil 75% e valor máximo de cada característica para a variante Iris versicolor:
iris.loc[iris['Species'] == 'Iris-versicolor'].describe()
| SepalLengthCm | SepalWidthCm | PetalLengthCm | PetalWidthCm | |
|---|---|---|---|---|
| count | 50.000000 | 50.000000 | 50.000000 | 50.000000 |
| mean | 5.936000 | 2.770000 | 4.260000 | 1.326000 |
| std | 0.516171 | 0.313798 | 0.469911 | 0.197753 |
| min | 4.900000 | 2.000000 | 3.000000 | 1.000000 |
| 25% | 5.600000 | 2.525000 | 4.000000 | 1.200000 |
| 50% | 5.900000 | 2.800000 | 4.350000 | 1.300000 |
| 75% | 6.300000 | 3.000000 | 4.600000 | 1.500000 |
| max | 7.000000 | 3.400000 | 5.100000 | 1.800000 |
Quantidade, média, desvio padrão, mínimo, quartil 25%, mediana, quartil 75% e valor máximo de cada característica para a variante Iris virginica:
iris.loc[iris['Species'] == 'Iris-virginica'].describe()
| SepalLengthCm | SepalWidthCm | PetalLengthCm | PetalWidthCm | |
|---|---|---|---|---|
| count | 50.00000 | 50.000000 | 50.000000 | 50.00000 |
| mean | 6.58800 | 2.974000 | 5.552000 | 2.02600 |
| std | 0.63588 | 0.322497 | 0.551895 | 0.27465 |
| min | 4.90000 | 2.200000 | 4.500000 | 1.40000 |
| 25% | 6.22500 | 2.800000 | 5.100000 | 1.80000 |
| 50% | 6.50000 | 3.000000 | 5.550000 | 2.00000 |
| 75% | 6.90000 | 3.175000 | 5.875000 | 2.30000 |
| max | 7.90000 | 3.800000 | 6.900000 | 2.50000 |
Diagrama de caixa
Podemos visualizar esses mesmos valores de uma forma gráfica por meio do diagrama de caixa. Wikipedia: "Em estatística descritiva, diagrama de caixa, diagrama de extremos e quartis, boxplot ou box plot é uma ferramenta gráfica para representar a variação de dados observados de uma variável numérica por meio de quartis."Diagrama de caixa
Wikipedia: "O box plot tem uma reta (whisker ou fio de bigode) que estende–se verticalmente ou horizontalmente a partir da caixa, indicando a variabilidade fora do quartil superior e do quartil inferior. Os valores atípicos ou outliers (valores discrepantes) podem ser plotados como pontos individuais. (...) Essa ferramenta é usada frequentemente para analisar e comparar a variação de uma variável entre diferentes grupos de dados."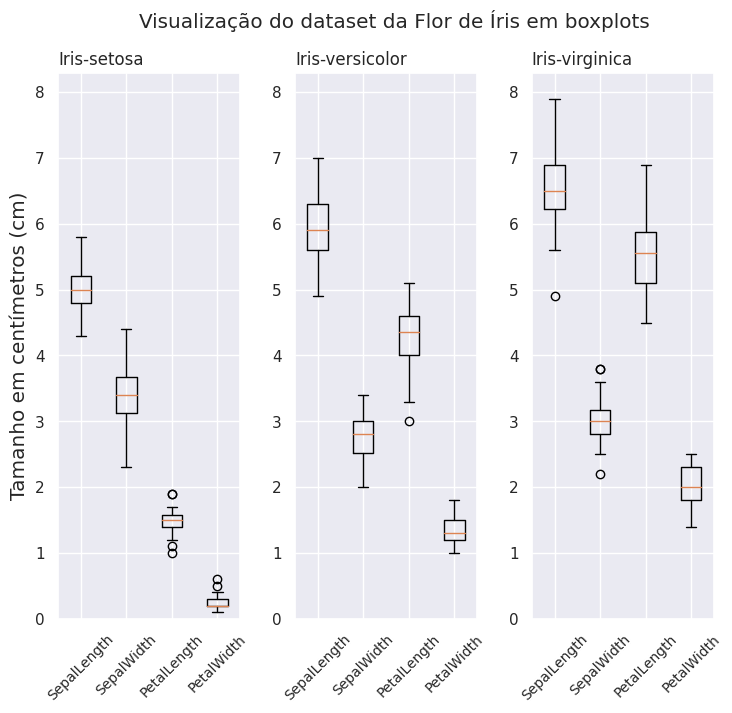
Na imagem anterior, podemos visualizar o valor lado a lado de cada característica observada para as três espécies numa mesma escada. Com os boxplots, vemos os valores máximos (traço superior), mínimos (traço inferior), discrepantes (círculos), a mediana (traço laranja central) e valores notáveis como 75% e 25% (limites superior e inferior das caixas).
Comparando os atributos correspondentes de cada espécie, podemos perceber que eles naturalmente se agrupam, evidenciando sua correlação.
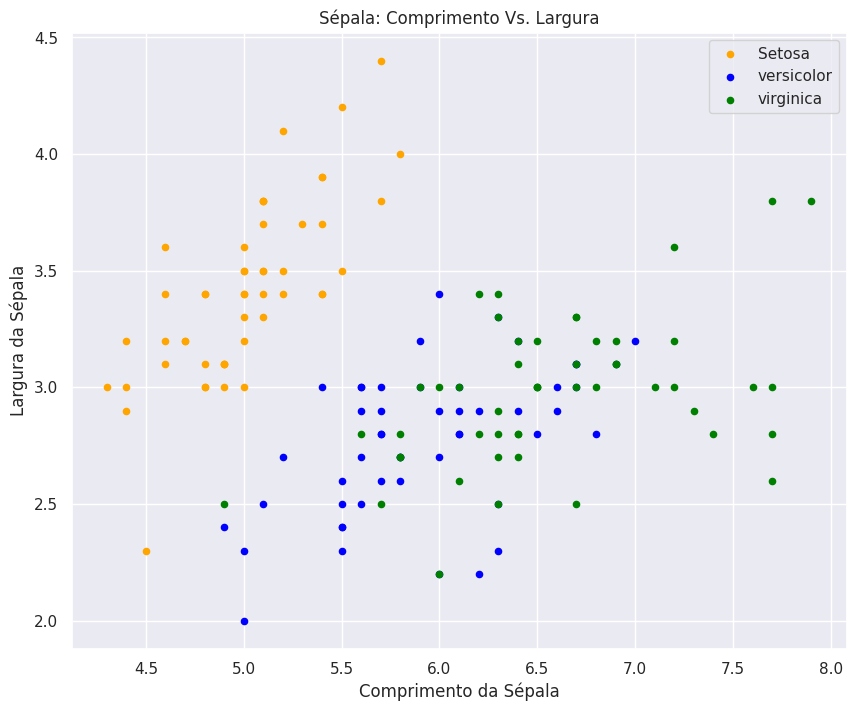
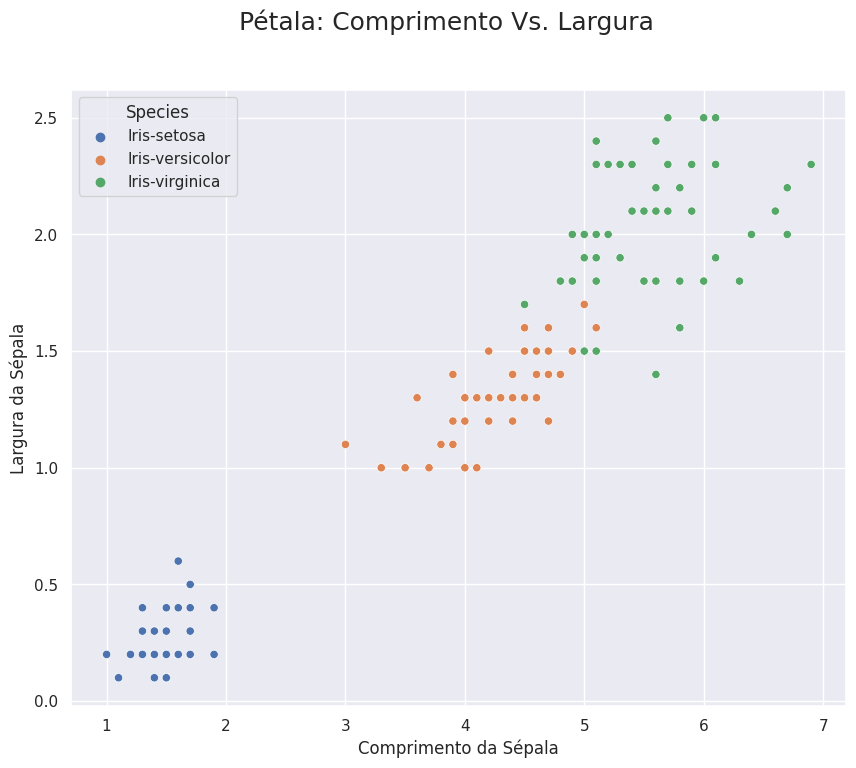
Utilizando um gráfico de regressão linear, podemos visualizar a função aproximativa das correlações:
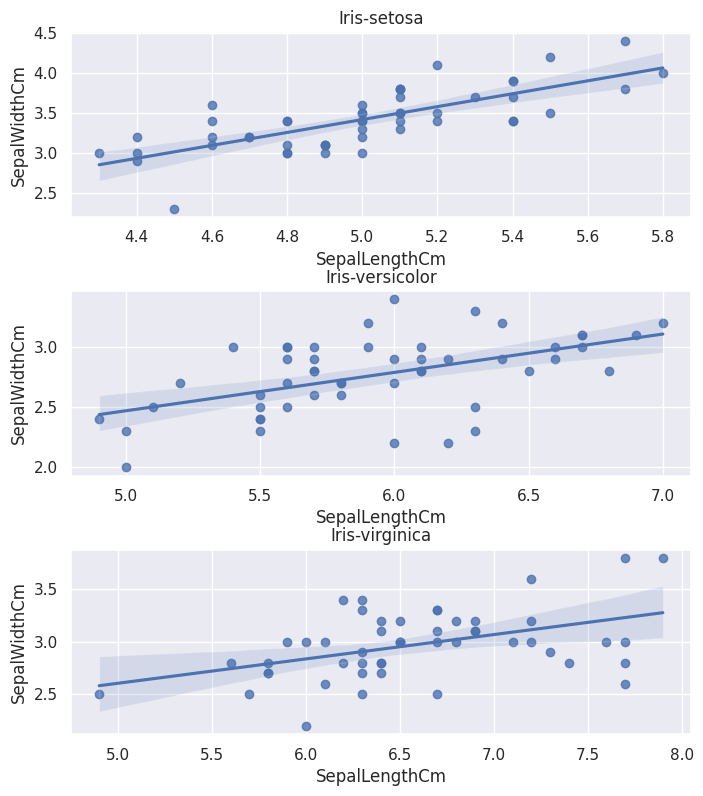
Também podemos usar gráficos de distribuição:
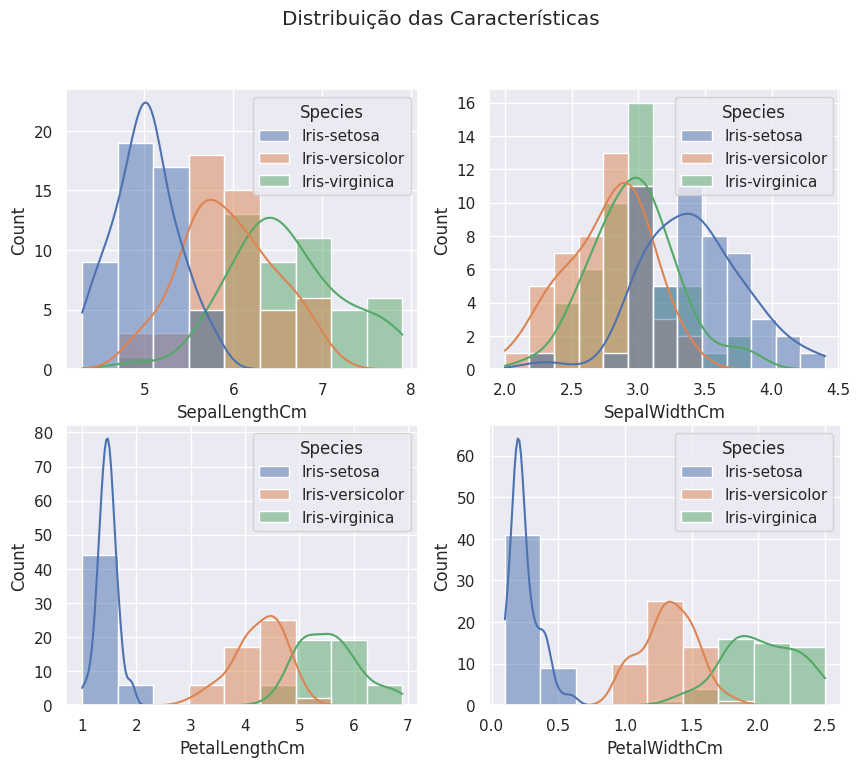
Comparando atributo por atributo, temos:
